Arány

Rövid összefoglalás az arányról:

Az arány két mennyiség viszonyát mutatja meg. Az arány, mivel törtekkel fejezzük ki egyszerűsíthető vagy bővíthető. (Vagyis 1:2 ugyanannyi, mint 2:4, mert 1/2 = 2/4-el. Így különböző számpároknak is lehet ugyanaz az aránya, például 1:2-höz ugyanazt jelenti, mint a 4:8-hoz vagy a 7:14-hez. Ezt könnyen megértheted, ha a törteket egyszerűsíted.) Nagyon fontos, hogy az arány nem fordítható meg, a megnevezéseket ugyanolyan sorrendben kell feltüntetni, mint a mennyiségeket. (Tehát az 1:2 nem egyenlő a 2:1 -el. A legegyszerűbb ha a meccsek eredményére gondolsz: ott is a csapatok sorrendjében mondod az eredményt, vagyis a Milan - Barca 2:1 azt jelenti, hogy a Milan 2 gólt rúgott, a Barca pedig 1-et. Nem mondhatod a számokat fordítva, mert az mást jelent.) Az animáción gyakorolhatod az arányokat, itt most a látható mennyiségeket kell írnod.

Arány és arányosság:

Az arány két szám egymáshoz való viszonyát fejezi ki, az arányosság pedig a két szám változását, ami történhet egyirányban (mindkettő nő vagy mindkettő csökken), ezt nevezzük egyenes arányosságnak, vagy ellentétesen (ha az egyik nő, akkor a másik csökken, vagy ha az egyik csökken akkor a másik nő), ezt nevezzük fordított arányosságnak. Tehát az arány két adott szám, az arányosság pedig egy folyamat, ahogy ez a két szám változik.

Egyenes arányosság:

Ha két mennyiség között az arányosság egyenes, az azt fejezi ki, hogy a két mennyiség együtt változik. Vagyis ha az egyiket növelem, a másik is nőni fog. Ilyen például a kert felásása és a ráfordított idő: minél tovább ásom, annál többet ások fel. Ilyenkor a mennyiségek hányadosa állandó, vagyis ha 1 perc alatt 2 m²-t ások fel, akkor 2 alatt 4-t, stb. Mivel 2:1=2 és 4:2=2.

Feladat:
Egy munkás egy órai munkájáért 400 Ft órabért kap. Mennyit fog kapni a nap végén, ha 8 órát dolgozott?
Megoldás következtetéssel: ha 1 óráért 400 Ft-ot kapott, akkor 8 óráért 8-szor ennyit fog kapni, vagyis 3200 Ft-ot.
Megoldás számítással:
(1) Mivel minél többet dolgozik annál többet keres, ezért ez egyenes arányosság.
(2) Az egyenes arányosságnál a két mennyiség hányadosa állandó.
(3) Az egyik mennyiség a munkaórák száma, a másik a kapott fizetés.
Nézd meg a megoldást, a hányadost osztásként és törtként is jeleztem. Mindegy melyiket használod.

\begin{align}400\colon&space;1&=&space;x\colon&space;8\nonumber\\\nonumber\\400&=&space;x\colon&space;8\nonumber\\\nonumber\\3200&=&space;x\nonumber\end{align}

\begin{align}\frac{400}{1}&=\frac{x}{8}\nonumber\\\nonumber\\400&=\frac{x}{8}\nonumber\\\nonumber\\3200&=&space;x\nonumber\end{align}

Fordított arányosság

Ha két mennyiség között az arányosság fordított, az azt fejezi ki, hogy a két mennyiség ellentétesen változik. Vagyis ha az egyiket növelem, akkor a másik csökkenni fog. Ilyen például a kert felásása és a dolgozók száma. Minél többen dolgoznak rajta, annál hamarabb végeznek. (Ha a dolgozók számát növelem, akkor a felásáshoz szükséges idő csökken.) Ilyenkor a mennyiségek szorzata állandó, vagyis ha 1 munkás alatt 12 nap alatt végez, akkor 2 munkás 6 nap alatt. Mivel 1*12=12 és 2*6=12

Feladat
Egy udvarban hatalmas halom sóder áll, amit az építkezésre kell szállítani. Egy teherautónak 12-szer kell fordulnia. Hányszor kell fordulniuk, ha 4 teherautót küldenek a sóderért?
Megoldás következtetéssel: Egy teherautó számára ez 12 szállítást jelent. Ha egyszerre 4 teherautó megy oda, akkor négyesével fogják vinni a sódert, ez összesen három szállítás a négy teherautónak. (Az első fordulóval 4 rakományt visznek el, a második fordulónál még 4-et, eddig összesen 8, a harmadik fordulónál még 4-et, ez összesen 12.)
Megoldás számítással:
(1) Minél több teherautó megy oda, annál kevesebbszer kell menniük, ezért ez fordított arányosság.
(2) A fordított arányosságnál a két mennyiség szorzata állandó.
(3) Az egyik mennyiség a teherautók száma, a másik mennyiség a fordulók száma.

\begin{align}1\cdot 12&=4\cdot x\nonumber\\\nonumber\\12\colon&space;4&=x\nonumber\\\nonumber\\3&=x\nonumber\end{align}

Érdekesség:

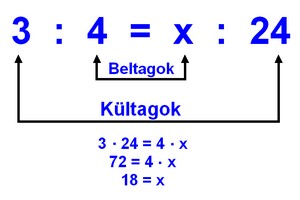
Két fogalom van, amit régebben tanítottak az iskolában ezekkel kapcsolatban. Az egyik a keresztbeszorzás, a másik a kültagok szorzata egyenlő a beltagok szorzatával. Mindkettő az egyenes arányosságra vonatkozik. A képeken láthatod a magyarázatot hozzá:

Az animáció a Math Is Fun weboldalról származik, köszönet az engedélyért!