Tengelyes tükrözés

A tengelyes tükrözés tulajdonságait próbálgathatod ebben az animációban.

Figyeld meg a következő tulajdonságokat:

• A tengelyes tükrözés megadható a tengellyel.
  (Más adatra nincs szükség, csak az alakzatra, amit tükrözni akarsz, és a tükörtengelyre. Ezután már csak egyféleképpen végezhető el a tükrözés.)
• A tengely minden pontjának tükörképe önmaga. (Vagyis a tükrözés során helyben maradnak, csak melléírjuk a tükörkép betűjelét is.)
• Minden szakasz egyenlő hosszúségú a tükörképével. (Röviden úgy mondjuk, hogy távtartó a tükrözés, a távolságok, hosszúságok ugyanakkorák maradnak.)
• Minden szög egyenlő nagyságú a tükörképével. (Szögtartó, a tükrözés során a szögek nagysága sem változik.)
• A tengelyes tükrözés megfordítja az alakzatok körüljárási irányát.
  (Ha az eredetiben a sorbajárva a betűk szerint a csúcsokat balról jobbra haladtál, akkor a tükörképében a betűk szerint jobbról balra fogsz haladni.
  Sárga nyíl mutatja a következő ábrán!)

Megjegyzés:
1. A pont és a tükörképe egyenlő távolságra van a tükörtengelytől. (Ennek az oka, amit az előbb mondtunk: a tükrözés távtartó.)
2. A pontot és a tükörképét összekötő szakasz merőleges a tükörtengelyre, ha a pont nem a tengelyen van. A szerkesztésnél meg fogod érteni...
(Ezt visszafelé is használhatjuk, ha a tükörtengelyt keressük: ha ismerjük a pontot és a tükörképét, akkor az őket összekötő szakasz felezőmerőlegese a tükörtengely.)

Betűzés

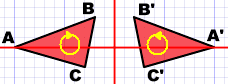
Betűvel jelöljük a síkidomok csúcsait, és felső vesszőt használunk,
hogy megkülönböztessük az eredetit a tükörképtől. (A tükörkép csúcsai kapják a vesszőt.)
Ez egy háromszög (ABC) és a tükörképe. (A'B'C')

Hogyan szerkesztjük?

Mindegyik csúcsponttal ugyanezt kell csinálni:

1. Szerkessz egy egyenest a csúcstól a tükörtengelyig, ami derékszöget zár be a tengellyel!	2. Hosszabbítsd meg a tengely másik oldalán! Vedd körzőnyílásba a csúcs és a tengely távolságát és mérd át a meghosszabbított egyenesre!	3. Kösd össze a kapott pontokat!

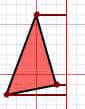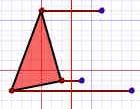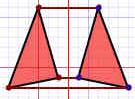Az animáció a Math Is Fun weboldalról származik, köszönet az engedélyért!